contra dancing, we'll ignore
those and think only about the transformations that do not change either the
shape or size of any geometric figure. These are called isometries.Geometric transformations
A geometric transformation changes the plane or 3-dimensional space. Each transformation can be defined by thinking about where it "takes" each point. Each point is said to be taken to its image.
Many kinds of transformations have proved useful enough have been given names, but for our purposes we need consider only reversible transformations of the plane. These transformations are reversible in the sense that no two points in the plane are taken to the same point, so there's no ambiguity about going backward. The technical term for reversible is invertible.
Among the invertible transformations are those that stretch or shrink the plane.
For contra dancing, we'll ignore
those and think only about the transformations that do not change either the
shape or size of any geometric figure. These are called isometries.
There are three kinds of isometries:
Reflections over a line take every point to a point directly across the line, as if the line were a mirror. More precisely, the image of a point P under a reflection over line L is on the line through P perpendicular to L and is the same distance from L as P is. In still other words, the line L is the perpendicular bisector of the segment between P and its image.
Translations are shifts of the entire plane. A translation along a vector (directed line segment) V takes every point P to the point at the head of a vector congruent to V whose tail is at P.
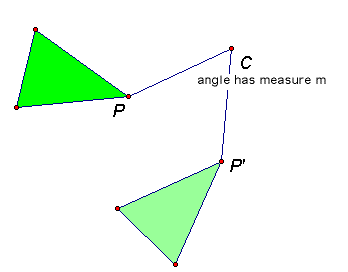
Rotations about a point rotate every other point in the plane around a single fixed point. Somewhat more formally, a rotation about center point C by angle of size m takes every point P to a point P' such that the angleP'CP has size m. A more rigorous definition would ensure that the orientation of each of these angles is the same.
Last update 20 August, 2005
