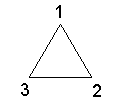Groups
Informally, a group is a set in which the combination of any two elements gives
another element in the set.
For a more technical definition, we have to specify what we mean by "combination"
(through a "binary operation"), and we need to specify reversibility
as well. So a more complete definition would be
A group under binary operation * is a set G with three properties:
1) for any two elements g and h in G, g*h
is also an element in G (closure);
2) there's an "identity element" e inG, meaning that,
for every element g in G, e*g = g*e
= g; and
3) every element g in G has an"inverse element"
g' in G, meaning that g*g' = g'*g
= e, the identity element.
Standard examples include
the integers (positive, negative, and 0) under binary operation addition.
(They don't form a group under multiplication, however, since property 3 is
not satisfied without introducing fractions. The non-negative integers under
addition satisfy properties 1 and 2 but not 3. The even integers satisfy property
1 under multiplication, but not property 2 or 3.)
the rational numbers (fractions, including all integers and negative
fractions) under binary operation addition. (They almost form a group under
multiplication; all that's missing is that 0 has no inverse element. The non-0
rational numbers form a group under multiplication.)
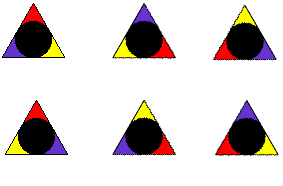
the symmetries of a geometric shape. A symmetry is a transformation
of the shape that places it on top of where it was originally.
Because 
contra dance figures
can be described in terms of symmetries, here's an exteded example. There
are six symmetries of an equilateral triangle. We can color the triangle to
show how it is transformed:
We can describe how the vertices are moved by numbering the three positions:
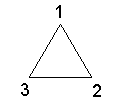
The transformation of the top left triangle to the third triangle of the
first row can be described by saying:
the vertex in position 1 goes to position 3;
the vertex in position 2 goes to position 1; and
the vertex in position 3 goes to position 2.
A shorthand for this transformation is (1 3 2).
The transformation of the top left triangle to the first triangle of the
second row can be represented by
the vertex in position 2 goes to position 3
the vertex in position 3 goes to position 2
A shorthand for this transformation is (2 3).
contra dancing
Larry Copes
Last modified 01-May-2002