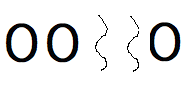
Combinatorics
Counting the number of ways of distributing 3 items among 3 bins.
First arrange the 3 items in some order. This can be done in 3! = 6 ways.
Now represent the 3 items in bins by a picture containing the 3 items (zeros) and the bin borders (squiggles). This picture represents 2 items in the first bin, none in the second, and one in the third:
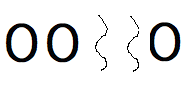
The number of ways of distributing the 3 items into the three bins is the same as the number of ways of choosing two of these five characters to be squiggles: 5C2 = 10.
Therefore there are 6 x 10 = 60 ways of distributing 3 items among 3 bins.
Last update 19-Jan-2003